Big Bang nucleosynthesis (BBN) into Lava-Void Cosmology

BBN in Lava-Void Cosmology: Unified Fluid Framework

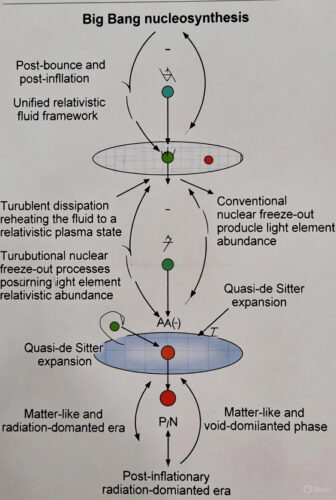By C. Rich

To integrate Big Bang nucleosynthesis (BBN) into Lava-Void Cosmology while adhering to the unified relativistic fluid framework, the post-bounce and post-inflationary evolution incorporates a radiation-dominated phase immediately following the viscous-driven quasi-de Sitter expansion. In this phase, turbulent dissipation at high densities reheats the fluid to a relativistic plasma state, where the effective equation of state approaches w = 1/3 and bulk viscosity becomes negligible. This ensures the expansion history during the BBN epoch (temperatures from approximately 10 MeV to 0.1 MeV, corresponding to timescales of seconds to minutes) closely replicates the standard hot Big Bang model, enabling conventional nuclear freeze-out processes to produce observed light element abundances.

The mechanism aligns with the model’s turbulence paradigm: Planck-scale intermittency and high Reynolds number flows during the bounce and inflation dissipate via cascade processes, converting coherent motion into thermal energy (reheating). As density dilutes below a transition threshold, the fluid transitions to ultra-relativistic behavior dominated by kinetic energy of vortex excitations (interpreted as relativistic particles), yielding $p \approx \rho/3$. Subsequently, further expansion leads to non-relativistic clustering (matter-like, $w \approx 0$) and void dominance ($w \approx -1$).

This approach preserves unification without separate components, inheriting the empirical success of standard BBN—one of the strongest pillars of conventional cosmology—while constraining parameters to minimize early-universe deviations. The baryon-to-photon ratio η is fixed by the clustered fraction of the fluid (viscous thickening), tuned to match observations (η ≈ 6 × 10^{-10} from Planck and BBN data).

Mathematical Formulation

Building on the viscous imperfect fluid equations from the inflationary integration:

The effective pressure remains with continuity:

To achieve radiation domination post-reheating, extend the density dependence as follows:

• Bulk viscosity decays rapidly after inflationary exit, e.g.,
  ensuring for (where is set below post-inflationary densities but above BBN-era densities).
• Barotropic pressure interpolates phases, with a relativistic term dominant at high densities. A suitable form is a modified generalized Chaplygin gas incorporating early radiation-like behavior:
  where provides a smooth step from ≈1 (radiation, high ρ) to ≈0 (transition to matter-like), and the negative term drives late acceleration. Parameters (A, α ≈ 0.8–1, β, ρ_mat) are tuned for observed transitions.

During the BBN era ($\rho \gg \rho_{\rm mat}$, $\xi \approx 0$), this yields $p_{\rm eff} \approx \rho / 3$, reducing the Friedmann and Raychaudhuri equations to standard radiation-dominated forms:

The temperature-expansion relation follows thermodynamically (assuming quasi-equilibrium post-reheating), with $T \propto a^{-1}$, and effective degrees of freedom $g_*$ emergent from turbulent excitations (tunable to match standard ≈10.75 during BBN).

Abundances are computed via the standard reaction network (e.g., neutron-proton freeze-out at T ≈ 1 MeV, deuterium bottleneck, etc.), yielding predictions consistent with observations($^4\text{He}$ mass fraction $Y_p \approx 0.247$, $\text{D/H} \approx 2.5 \times 10^{-5}$, $^7\text{Li/H} \approx 5 \times 10^{-10}$) when η matches constraints. Extensions of existing numerical simulations (integrating modified Friedmann equations backward from late times) can verify negligible deviations (<1% in expansion rate) during BBN, constraining parameters tightly.

This extension maintains philosophical coherence (fluid dynamics across epochs) and resolves the identified omission, with potential for distinguishable signatures in high-precision future BBN probes if small viscous residuals persist.

C. Rich